Bet I Can Make Uxcum Again
Dy 8 x + sin(iii X) - 5dx2 y2+ii y-3Rewrite the equation with ten and dx on 1 side, Y and dy on the other side: Integrate and solve the differential equation:
dy 8 10 + sin(iii X) - 5 dx 2 y2+2 y-3 Rewrite the equation with x and dx on i side, Y and dy on the other side: Integrate and solve the differential equation:

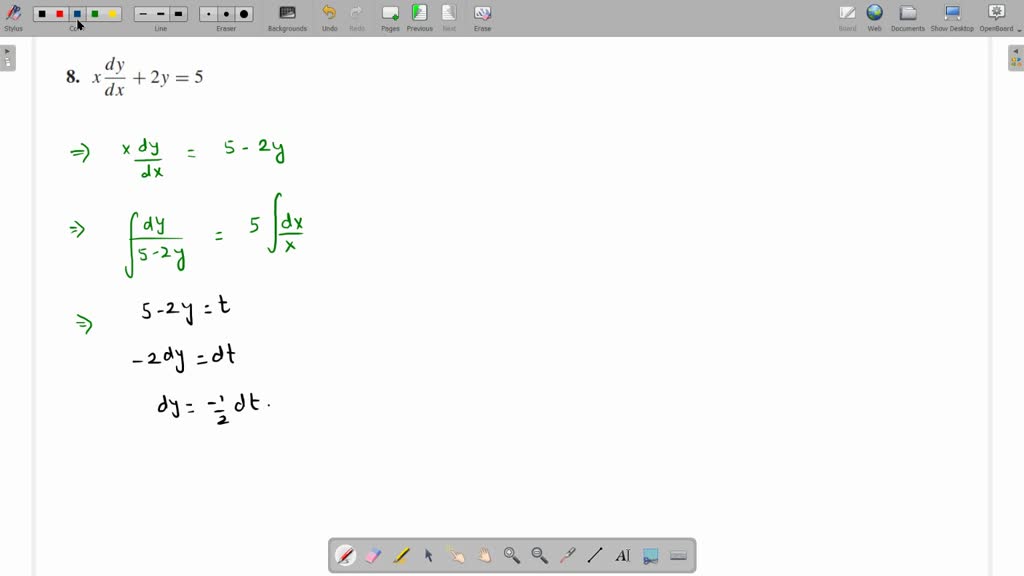
Solve each differential equation. $$ \text { eight. } x \frac{d y}{d x}+2 y=5 $$
Hullo Friends. We have to solve that given defense force electrician's a weekend. I did do you to purchase upon D. X foursquare plus develop on the X months of information technology very close to zero. This is the second guild homogeneous equation. And so we tin can also write it similar this. This car vipers split monastery very close to zero. So actually a question will exist like this. I was actually a question about this baby. Mm square anoint em month fourscore calls to nothing. Okay, then the rules of the seclusion will exist A homo and M two. So that is a cost to and one is -1 Plus Square Root of 33.ii. Mt will exist direction manners of schools of 33 upon to. Okay, this is the rules of the other equation. And so we can write the solution vehicles to seven and so seven into even to the power of and annex policy too. Y'all practice the ability of M two ten. Okay, so we tin make up one's mind via calls to 7 into into the power of management minus one plus the square root of 33 upon two of X. Plus you two into into the power minus one minus of this courtroom of 33 upon two of ten. Mhm. Mhm. And so why volition be costume U to the power of -X. Y. two is common seven into it. To the Pavlov Square root of 33 to upon X. Placido into 2 departments of the square root of 33 upon ii of X. So this is the answer. So mm I hope you understood.
This question asked the states to solve the differential equation three. X squared y squared Non what nosotros know is that if this is r d y o ver de axe than r D y over, why squared is three x squared DX. This allows the states to get the X is on the aforementioned side and the wise on the same side. No, let's accept the integral. The integral of this is negative one over. Why be integral off this increased exports by one divide by the new exponents is execute. Don't forget our abiding of integration plus C now lastly to right this just in terms of why we get wise negative i divided by X cubed plus sissy
Alright this question covers topics relating to start club differential equations. The vulnerable equations. Kickoff you need to fact arrived the right manus side. Right subsequently finalizing the right hand side and yous take this equation correct? That means you need to you lot have to re written this equation equally why? Minus two divided by y over three. The y equals two X minus 1 divided by x plus four D. 10. Okay. And now you accept the intolerable size, you take the intolerable sides like this. Right? And from here you tin easily use the potential fraction right? Then yous're right, ane man is equal to one minus three and minus Y plus iii in minus five over this D. Y. And the aforementioned matter for X. 10 plus iv and so minus phi of X plus four Ds. Okay and now yous do the integration is equal to ane minus five over White last iii D. Y. Because to the interest of one plus 1 minus 5 over X plus four dx. Okay so. So hither you have Y -five times Times a lot of absolute failure. White Plus three echo two x minus phi time, accented lots of absolute value of X plus 4 plus some constant. Right? And then you? Re written it as y echo to find We go to X-plus 5 log of y plus three over Ten plus four. Right? Yous plus some constant. So this is your solution
And this question nosotros need to observe uh find a solution of the differential equation by separation of vehicles. Let'south first try to simplify this, we have dy over dx and this is equal to ten, Y plus three, Ten minus y minus three minus y minus three over xy minus 2, X plus four, Y plus or y minus Z. Uh Then this can be written every bit de vie or D Ten is equal to uh Nosotros're here, let's try to factories this. So we take Ten out from hither, then we have y plus three and nosotros take minus one out from here and we are left at 5 plus three. Again over Here we accept Ten out. And then we are left with via -2 and nosotros're here we accept four out. So we are again left via -2. And so this tin can be read on us, contend over dx is equal to If you take wire plus three out, mm Y plus three is a mutual factor, Nosotros are left with x minus one. And if we take y minus two as a common gene, we are left with X plus for over here. Uh Let'south come across, let's try to cantankerous multiply this and bring the terms with the same variable over to one side. So this can be written as y minus two over y plus three D. Y. And this is equal to x minus one over 10 plus four D X. This is how it looks like. And then this can we read written equally the left hand side and the right paw side tin can read it. And uh since the denominators common. So uh let's write the numerator as Y plus three minus five. So what nosotros take done is nosotros take written minus two as 3 minus five considering three minus five is nothing just minus two. Or via street. We're talking a infinitesimal nearly Hawaii are nosotros doing this? So let's write these terms showtime. And also I'm writing x minus one has X plus four minus +54 minus five is again minus one over X plus four dx. So why are we doing this? That's considering I want to bring the term which is in denominator in the numerator equally well. So there is a Y plus three denominator. I demand to get Y plus three. Somehow in the numerator and there is an X plus four. I need to get an X plus 4 in the numerator. Where is the do good of this? Because at present if we segregate the terms, this can be written as Y plus three over Y plus three. Since the denominators mutual minus y minus v over Y plus three. And this is where divide this is equal to likewise X plus 4 over X plus four minus five over X plus four. And over here we have uh B. 10. So this can be written as Y plus 3, Y plus threes cancer really for the one. And then one minus v over Y plus 3 D. Y. This is equal to ane minus five over X plus four D Ten. And this can exist separated as uh integration of dy minus five. Dy over Y plus 3 is equal to dx minus five D ten. Or X plus four. So now this can be integrated on on all the sides, on both the sides. So the integration or D Y. Southward. Married woman five is a abiding. That comes out integration of diva over via plus 3 is natural police via plus three zip. To integration of dx sx minus five is a constant. Again, information technology comes out integration is natural log of X plus floor extras for is the constant of integral. Asi. And then this is the final. Also, thank you.
3 answers
A researcher has recently developed a new scale that measures self perceieved "coolness". since this is a new scale, there is no population level information about the hateful. suppose ix individuals are measured on this scale and the post-obit scotes are recorded: 82, 99, 68, 66, 75, 78, 55, 77, 52 calculate a 95% conviction interval for mu, the population hateful a) (64.08, lxxx.81)b) (62.07, 82.82)c) (61.44, 83.44)d) (63.57, 81.31)
a researcher has recently developed a new scale that measures self perceieved "coolness". since this is a new scale, there is no population level information about the mean. suppose ix individuals are measured on this scale and the following scotes are recorded: 82, 99, 68, 66, 75, 78, 55, ...
septimusbehonell87.blogspot.com
Source: https://itprospt.com/num/1961967/dy-8-x-sin-3-x-5dx2-y2-2-y-3rewrite-the-equation-with-x